A universal quantum algorithm for weighted maximum cut and Ising problems

Natacha Kuete Meli, Florian Mannel and Jan Lellmann

Abstract:

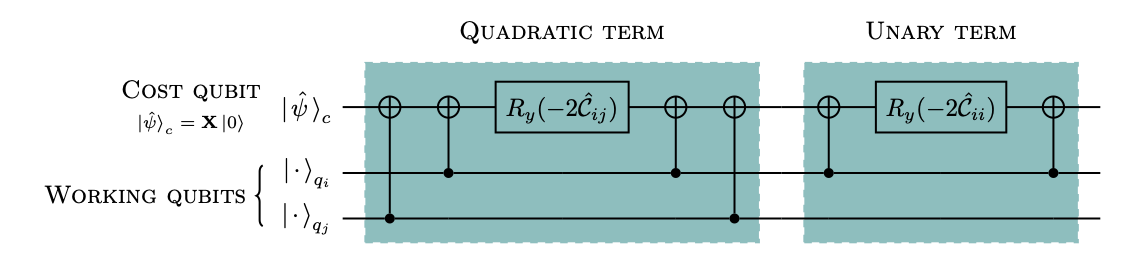
We propose a hybrid quantum-classical algorithm to compute approximate solutions of binary combinatorial problems. We employ a shallow-depth quantum circuit to implement a unitary and Hermitian operator that block-encodes the weighted maximum cut or the Ising Hamiltonian. Measuring the expectation of this operator on a variational quantum state yields the variational energy of the quantum system. The system is enforced to evolve toward the ground state of the problem Hamiltonian by optimizing a set of angles using normalized gradient descent. Experimentally, our algorithm outperforms the state-of-the-art quantum approximate optimization algorithm on random fully connected graphs and challenges D-Wave quantum annealers by producing good approximate solutions.

Ressources

[pdf] [arxiv] [github]

Cite [BibTex]:

@article{kuete2023universal,
  title={A universal quantum algorithm for weighted maximum cut and Ising problems},
  author={Kuete Meli, Natacha and Mannel, Florian and Lellmann, Jan},
  journal={Quantum Information Processing},
  volume={22},
  number={7},
  pages={279},
  year={2023},
  publisher={Springer}
}